Материал по математике по теме "Теория вероятностей"

Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.

События. Виды событий

Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными.

Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания. Пример невозможного события: в условиях земного тяготения подброшенная монета улетит вверх.

И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила/направление броска, сопротивление воздуха и т.д.

Подчёркнутый критерий случайности очень важен – так, например, карточный шулер может очень ловко имитировать случайность и давать выигрывать жертве, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.

Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.

Полную информацию смотрите в файле.

Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей^[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)^[2].

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.

События. Виды событий

Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными.

Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания. Пример невозможного события: в условиях земного тяготения подброшенная монета улетит вверх.

И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл».  В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила/направление броска, сопротивление воздуха и т.д.

Подчёркнутый критерий случайности очень важен – так, например, карточный шулер может очень ловко имитировать случайность и давать выигрывать жертве, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.

Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.

События (любые) обозначают большими латинскими буквами 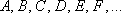 либо теми же буквами с подстрочными индексами, например: 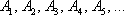. Исключение составляет буква 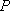, которая зарезервирована под другие нужды.

Запишем следующие случайные события:

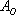 – в результате броска монеты выпадет «орёл»;
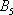 – в результате броска игральной кости (кубика) выпадет 5 очков;
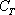 – из колоды будет извлечена карта трефовой масти (по умолчанию колода считается полной).

Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).

Следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле снова показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие 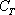 становится невозможным. Наоборот, если испытателю известно, что, например, дама треф лежит снизу, то он при желании может сделать событие  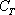достоверным =) Таким образом, в данном примере предполагается, что карты хорошо перемешаны и их рубашки неразличимы, т.е. колода не является краплёной. Причём, здесь под «крапом» понимаются даже не «умелые руки», ликвидирующие случайность вашего выигрыша, а видимые дефекты карт. Например, рубашка той же дамы треф может быть грязной, порванной, заклеенной скотчем… блин, какое-то пособие для начинающего чикатило получилось =)

Таким образом, при розыгрыше важного жребия всегда есть смысл невзначай посмотреть, а не одинаковы ли грани монеты ;-)

Другая важная характеристика событий – это их равновозможность. Два или бОльшее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другие. Например:

выпадение орла или решки при броске монеты;
выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
извлечение карты трефовой, пиковой, бубновой или червовой масти из колоды.

При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.

Могут ли быть те же события не равновозможными? Могут! Например, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Как говорится, ещё одна лазейка для мошенников. События 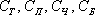 – извлечение трефы, пики, червы или бубны тоже равновозможны. Однако равновозможность легко нарушит фокусник, который, тасуя колоду (даже «идеальную»), ловко подсмотрит и спрячет в рукаве, например, туза треф. Здесь становится менее возможным, что оппоненту будет сдана трефа, и, главное, менее возможно, что будет сдан туз.

Тем не менее, в рассмотренных трёх случаях при потере равновозможности всё же сохраняется случайность событий.

Совместные и несовместные события. Противоположные события.
Полная группа событий

События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий  является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой вверху. Например:

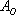 – в результате броска монеты выпадет орёл;
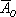 – в результате броска монеты выпадет решка.

Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.

Противоположные события легко формулируются из соображений элементарной логики:

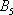 – в результате броска игрального кубика выпадет 5 очков;
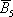 – в результате броска игрального кубика выпадет число очков, отличное от пяти.

Либо пять, либо не пять – третьего не дано, т.е. события несовместны и противоположны.

Аналогично – или трефа или карта другой масти:

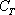 – из колоды будет извлечена карта трефовой масти;
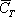 – из колоды будет извлечена пика, черва или бубна.

Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу. Однако в различных задачах с одним и тем же объектом могут фигурировать разные события, например, для игрального кубика характерно рассмотрение следующего набора:

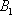 – в результате броска игрального кубика выпадет 1 очко;
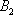 – … 2 очка;
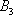 – … 3 очка;
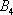 – … 4 очка;
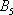 – … 5 очков;
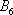 – … 6 очков.

События 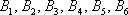 несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).

Ещё одно важное понятие, которое нам скоро потребуется – это элементарность исхода (события). Если совсем просто, то элементарное событие «нельзя разложить на другие события». Например, события 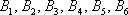 элементарны, но событие  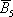не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).

В примере с картами события 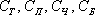 (извлечение трефы, пики, червы или бубны соответственно) несовместны и образуют полную группу, но они неэлементарны. Если считать, что в колоде 36 карт, то каждое из перечисленных событий включает в себя 9 элементарных исходов. Аналогично – события  (извлечение шестёрки, семёрки, …, короля, туза) несовместны, образуют полную группу и неэлементарны (каждое включает в себя 4 исхода).

Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и, разумеется, 36 несовместных элементарных исходов тоже образуют полную группу событий.

Совместные события менее значимы с точки зрения решения практических задач, но обходить их стороной не будем. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:

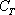 – из колоды карт будет извлечена трефа;
 – из колоды карт будет извлечена семёрка.

Если быть совсем лаконичным, одно не исключает другого.

Понятие совместности охватывает и бОльшее количество событий:

 – завтра в 12.00 будет дождь;
 – завтра в 12.00 будет гроза;
 – завтра в 12.00 будет солнце.

Ситуация, конечно, довольно редкая, но совместное появление всех трёх событий в принципе не исключено. Следует отметить, что перечисленные события совместны и попарно, т.е. может быть только ливень с грозой или грибной дождик, или погромыхает неподалёку на фоне ясного неба.

Алгебра событий

Мужайтесь, будет и матан =)

Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:

Операция сложения событий означает логическую связку ИЛИ,
а операция умножения событий – логическую связку И.

1) Суммой двух событий  и  называется событие  которое состоит в том, что наступит или событие  или событие  или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие  или событие .

Правило распространяется и на бОльшее количество слагаемых, например, событие  состоит в том, что произойдёт хотя бы одно из событий , а если события несовместны – то одно и только одно событие из этой суммы: или событие , или событие , или событие , или событие , или событие .

Примеров масса:

События  (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

Событие  (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

Событие  (будет чётное число очков) состоит в том, что выпадет или 2 или 4 или 6 очков.

Событие  заключается в том, что из колоды будет извлечена карта красной масти (черва или бубна), а событие  – в том, что будет извлечена «картинка» (валет или дама или король или туз).

Чуть занятнее дело с совместными событиями:

Событие  состоит в том, что из колоды будет извлечена трефа или семёрка или семёрка треф. Согласно данному выше определению, хотя бы что-то – или любая трефа или любая семёрка или их «пересечение» – семёрка треф. Легко подсчитать, что данному событию соответствует 12 элементарных исходов (9 трефовых карт + 3 оставшиеся семёрки).

Событие  состоит в том, что завтра в 12.00 наступит ХОТЯ БЫ ОДНО из суммируемых совместных событий, а именно:

– или будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.

То есть, событие  включает в себя 7 возможных исходов.

Второй столп алгебры событий:

2) Произведением двух событий  и  называют событие , которое состоит в совместном появлении этих событий, иными словами, умножение  означает, что при некоторых обстоятельствах наступит и событие , и событие . Аналогичное утверждение справедливо и для бОльшего количества событий, так, например, произведение  подразумевает, что при определённых условиях произойдёт и событие , и событие , и событие , …, и событие .

Рассмотрим испытание, в котором подбрасываются две монеты и следующие события:

 – на 1-й монете выпадет орёл;
 – на 1-й монете выпадет решка;
 – на 2-й монете выпадет орёл;
 – на 2-й монете выпадет решка.

Тогда:
– событие  состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орёл;
– событие  состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;
– событие  состоит в том, что на 1-й монете выпадет орёл и на 2-й монете решка;
– событие  состоит в том, что на 1-й монете выпадет решка и на 2-й монете орёл.

Нетрудно заметить, что события  несовместны (т.к. не может, например, выпасть 2 орла и в то же самое время 2 решки) и образуют полную группу (поскольку учтены все возможные исходы броска 2-х монет). Давайте просуммируем данные события: . Как интерпретировать эту запись? Очень просто – умножение означает логическую связку И, а сложение – ИЛИ. Таким образом, сумму  легко прочитать понятным человеческим языком: «выпадут два орла или две решки или на 1-й монете выпадет орёл и на 2-ой решка или на 1-ой монете выпадет решка и на 2-й монете орёл »

Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае – две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:

 – в 1-м броске выпадет 4 очка;
 – во 2-м броске выпадет 5 очков;
 – в 3-м броске выпадет 6 очков.

Тогда событие  состоит в том, что в 1-м броске выпадет 4 очка и во 2-м броске выпадет 5 очков и в 3-м броске выпадет 6 очков. Очевидно, что в случае с кубиком будет значительно больше комбинаций (исходов), чем, если бы мы подбрасывали монету.

…Понимаю, что, возможно, разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько анонимов, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали =)

Вероятность события

Вероятность события – это центральное понятие теории вероятностей. …Убийственно логичная вещь, но с чего-то надо было начинать =)  Существует несколько подходов к её определению:

Классическое определение вероятности;
Геометрическое определение вероятности;
Статистическое определение вероятности.

В данной статье я остановлюсь на классическом определении вероятностей, которое находит наиболее широкое применение в учебных заданиях.

Обозначения. Вероятность некоторого события  обозначается большой латинской буквой 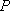, а само событие берётся в скобки, выступая в роли своеобразного аргумента. Например:

 –  вероятность того, что в результате броска монеты выпадет «орёл»;
 – вероятность того, что в результате броска игральной кости выпадет 5 очков;
 – вероятность того, что из колоды будет извлечена карта трефовой масти.

Также для обозначения вероятности широко используется маленькая буква . В частности, можно отказаться от громоздких обозначений событий  и их вероятностей  в пользу следующей стилистики::

 – вероятность того, что в результате броска монеты выпадет «орёл»;
 – вероятность того, что в результате броска игральной кости выпадет 5 очков;
 – вероятность того, что из колоды будет извлечена карта трефовой масти.

Данный вариант популярен при решении практических задач, поскольку позволяет заметно сократить запись решения. Как и в первом случае, здесь удобно использовать «говорящие» подстрочные/надстрочные индексы.

Все уже давно догадались о числах, которые я только что записал выше, и сейчас мы узнаем, как они получились:

Классическое определение вероятности:

Вероятностью наступления события  в некотором испытании называют отношение , где:

 – общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;

 – количество элементарных исходов, благоприятствующих событию .

При броске монеты может выпасть либо орёл, либо решка – данные события образуют полную группу, таким образом, общее число исходов ; при этом, каждый из них элементарен и равновозможен.  Событию 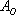 благоприятствует  исход (выпадение орла). По классическому определению вероятностей: .

Аналогично – в результате броска кубика может появиться  элементарных равновозможных исходов, образующих полную группу, а событию 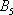 благоприятствует единственный  исход (выпадение пятёрки). Поэтому: .

Особое внимание обращаю на третий пример. Здесь будет некорректным сказать «раз в колоде 4 масти, то вероятность извлечения трефы ». В определении речь идёт об элементарных исходах, поэтому правильный порядок рассуждений таков: всего в колоде 36 карт (несовместные элементарные исходы, образующие полную группу), из них 9 карт трефовой масти (кол-во элементарных исходов, благоприятствующих событию 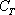); по классическому определению вероятности: . Именно так!

Вероятности можно выразить и в процентах, например: вероятность выпадение орла равна , выпадения пятёрки , извлечения трефы , но в теории вероятностей ЭТОГО ДЕЛАТЬ НЕ ПРИНЯТО (хотя не возбраняется прикидывать проценты в уме).

Принято использовать доли единицы, и, очевидно, что вероятность может изменяться в пределах . При этом если , то событие  является невозможным, если  – достоверным, а если , то речь идёт о случайном событии.

! Если в ходе решения любой задачи у вас получилось какое-то другое значение вероятности – ищите ошибку!

При классическом подходе к определению вероятности крайние значения (ноль и единица) получаются посредством точно таких же рассуждений. Пусть из некой урны, в которой находятся 10 красных шаров, наугад извлекается 1 шар. Рассмотрим следующие события:

 – из урны будет извлечён красный шар;
 – из урны будет извлечён зелёный шар.

Общее количество исходов: . Событию  благоприятствуют все возможные исходы , следовательно, , то есть данное событие достоверно. Для 2-го же события благоприятствующие исходы отсутствуют , поэтому , то есть событие  невозможно.

Особый интерес представляют события, вероятность наступления которых чрезвычайно мала. Хоть такие события и являются случайными, для них справедлив следующий постулат:

в единичном испытании маловозможное событие не произойдёт.

Именно поэтому Вы не сорвёте в лотерее Джек-пот, если вероятность этого события, скажем, равна  0,00000001. Да-да, именно Вы – с единственным билетом в каком-то конкретном тираже. Впрочем, бОльшее количество билетов и бОльшее количество розыгрышей Вам особо не помогут. ...Когда я рассказываю об этом окружающим, то почти всегда в ответ слышу: «но ведь кто-то выигрывает». Хорошо, тогда давайте проведём следующий эксперимент: пожалуйста, сегодня или завтра купите билет любой лотереи (не откладывайте!). И если выиграете... ну, хотя бы больше 50-ти килорублей, обязательно отпишитесь – я объясню, почему это произошло. За процент, разумеется =) =)

Но грустить не нужно, потому что есть противоположный принцип: если вероятность некоторого события очень близка к единице, то в отдельно взятом испытании оно практически достоверно произойдёт. Поэтому перед прыжком с парашютом не надо бояться, наоборот – улыбайтесь! Ведь должны сложиться совершенно немыслимые и фантастические обстоятельства, чтобы отказали оба парашюта. 

Хотя всё это лирика, поскольку в зависимости от содержания события первый принцип может оказаться весёлым, а второй – грустным; или вообще оба параллельными.

Пожалуй, пока достаточно, на уроке

Задачи на классическое определение вероятности мы выжмем максимум из формулы . В заключительной же части этой статьи рассмотрим одну важную теорему:

Сумма вероятностей событий, которые образуют полную группу, равна единице. Грубо говоря, если события образуют полную группу, то со 100%-й вероятностью какое-то из них произойдёт. В самом простом случае полную группу образуют противоположные события, например:

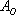 – в результате броска монеты выпадет орёл;
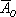 – в результате броска монеты выпадет решка.

По теореме:  

Совершенно понятно, что данные события равновозможны и их вероятности одинаковы .

По причине равенства вероятностей равновозможные события часто называют равновероятными. А вот и скороговорка на определение степени опьянения получилась =)

Пример с кубиком: события  противоположны, поэтому .

Рассматриваемая теорема удобна тем, что позволяет быстро найти вероятность противоположного события. Так, если известна вероятность  того, что выпадет пятёрка, легко вычислить вероятность того, что она не выпадет:

Это гораздо проще, чем суммировать вероятности пяти элементарных исходов. Для элементарных исходов, к слову, данная теорема тоже справедлива:

События 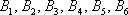, как отмечалось выше, равновозможны – и теперь мы можем сказать, что равновероятны. Вероятность выпадения любой грани кубика равна :

Ну и на закуску колода: поскольку нам известна вероятность  того, что будет извлечена трефа, то легко найти вероятность того, что будет извлечена карта другой масти:

Заметьте, что рассмотренные пары событий  и  не равновероятны, как оно чаще всего и бывает.

В упрощенной версии записи решения вероятность противоположного события стандартно обозначается строчной буквой . Например, если  – вероятность того, что стрелок попадёт в цель, то  – вероятность того, что он промахнётся.